200以上 double integral of e^(-x^2-y^2) 817685-Double integral of exp(-x^2 - y^2)
Question Solve The Double Integral Of E^(x^3) Dx Dy X From Sqrt(y) To 2, Y From 0 To 4 This problem has been solved!Mar 12, 15 · How do you calculate the double integral of #f(x,y) = 28y(e^x)# over the triangle indicated by the following points (0,0), (4,1), and (4,3)?To have two limits in double integral?

Integration Of E X 2 Page 3 Line 17qq Com
Double integral of exp(-x^2 - y^2)
Double integral of exp(-x^2 - y^2)-A surface integral generalizes double integrals to integration over a surface (which may be a curved set in space);Dx $$ a) Sketch the region of integration b) Convert the double integral into a Type II double integral




Solved Show How To Calculate The Iterated Integral Integ Chegg Com
Feb 19, 18 · int_2^3 \ e^(x^2) \ dx ~~ This cannot be computed using known elementary functions It would require a numerical approximation Using such a method we obtain int_2^3 \ e^(x^2) \ dx ~~Double integration in R with additional argument But I'm still confused how I can get my question from those answers My question is following I would like to code this calculations in R From my hand and Wolfram alpha calculation, it becomes 1664 I know how to take a integral if both integrals are from exact numbers using adaptIntegrate()Get the free "Polar Integral Calculator" widget for your website, blog, Wordpress, Blogger, or iGoogle Find more Mathematics widgets in WolframAlpha
My dear friend The integration of e to the power x of a function is a general formula of exponential functions and this formula needs a derivative of the given function This formula is important in integral calculus The integration of e to the pSolution for Given the double integral ffp(ry)e** v° dxdy, where D = {(x, y) 0 < xyOct 11, 12 · The integrand is separableie a function of x times a function of y So the double integral is the product of the integrals 1 ∫ e^(3x) dx = (1/3)(e 1)
As the night goes on the indefinite integral offers to buy the two another round, but the definite integral politely declinesCompute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, historyJun 07, · Calculating double integral for exponential function Follow 6 views (last 30 days) Malena Vasquez on 7 Jun Vote 0 ⋮ Vote 0 Commented Malena Vasquez on 7 Jun Accepted Answer madhan ravi Hi everyone!




Linear Algebra Sheet 6 Summer 19 Studocu




Solved A Using Polar Coordinates Evaluate The Improper Chegg Com
Calculate the double integral R={(x,y) 0 (less than or equal to) x (less than or equal to) 4, 0 (less than or equal to) y (less than or equal to) 1} *Response times vary by subject and question complexity Median response time is 34 minutes and may beSep 21, 05 · double integral sign The double integral sign is used to indicate mathematical integration performed twice in succession Double integrals are used to calculate the integral s of function s in two variable s An example is the volume under a surface inIt can be thought of as the double integral analog of the line integral The function to be integrated may be a scalar field or a vector field The value of the surface integral is the sum of the field at all points on the surface




Double Integration



Archive Image From Page 27 Of Directivity Function Of A General Directivity Function Of A General Receiving Array For Spherical And Plane Sound Waves Directivityfunct00warn Year 1961 B Rectangular Area Applying Equation
To change variables in a double integral such as $$\iint_\dlr f(x,y) dA,$$ one uses a mapping of the form $(x,y) = \cvarf(\cvarfv,\cvarsv)$ This function maps some region $\dlr^*$ in the $(\cvarfv,\cvarsv)$ coordinates into the original region $\dlr$ of the integral in $(x,y)$ coordinatesCalculus Introduction to Integration Integrals of Exponential Functions 1 Answer Gió Mar 12, 15 Try this hope it helps Answer linkWhile simulating the value of a double integral , why do we need to draw different samples everytime?



Evaluate A Double Integral Over A General Region With Substitution F X Y E X Y Youtube




Solved Question 2 5 Points Compute The Double Integral Chegg Com
Then, via the usage of these outcomes, theConsider the double integral $$\int_0^1 \int_0^{e^x} \sqrt{1 e^x} \;Sep 11, 10 · You have a double integral For the inside integral, you are integrating with respect to y (hence dy) Everything except y's are treated as constants So pretend x is like the number 2 thus INT (xe^(xy)dy) becomes x* int (e^xy)dy What is the integral of e^(2x) that is e^2x /2 c Thus the inner integral becomes x*1/x *e^(xy) C1




Btech Ii Engineering Mathematics Unit3




Solved Use Polar Coordinates To Evaluate The Double Integ Chegg Com
Jun 05, 04 · An integral representation of a function is an expression of the function involving a contour integral Various integral representations are known for many special functions Integral representations can be important for theoretical reasons, eg giving analytic continuation or functional equations, or sometimes for numerical evaluationsThe integral I calculated was $$\int_0^y\int_x^\infty e^{(xy)}dydx$$Consider the doubleintegral Where is bounded by the lines Because x is raised to a higher power in one of the equations and y is not, I will set up y as a function of x Now equate the lines and The region is and Chapter 153, Problem 18E is solved View this answer View this answer View this answer done loading




Express Each Double Integral Over The Given Region R As An Iterated Integral Integral Triangle




Answered In 7 Sovle V 2 Sin 2 E 1 Bartleby
The convolution theorem with an evidence is mentioned;Double integral definition, an integral in which the integrand involves a function of two variables and that requires two applications of the integration process to evaluate See moreBackground Cellulite is a serious cosmetic concern for most of the 90% of women affected by it Objective To assess the clinical efficacy of a complex integral anticellulite gel Methods This doubleblind, randomized, placebocontrolled study involved 44 healthy women, aged 2555 years Subjects had a normal to slightly overweight body mass index and presented slight to moderate




Integration Of E X 2 Page 3 Line 17qq Com




Integral Of Xy 2 Page 1 Line 17qq Com
Should I convince my advisor that thesis work is not finished yetI'm trying to calculate this integral using Matlab but, being a beginner, I'm struggling a bitOct 11, 12 · integralIntegral(e^(3x4y))dydx first integrate wrt y so we are left with Integral( e^(3x)*e^(4y)/4)dx now integrate wrt x e^(3x4y)/12 C



What Is The Integration Of E X 2 Dx Over The Limit From 0 To 1 How Do You Solve It Quora




Evaluate The Double Integral Double Integral X 2 2y Da D Is Bounded By Y X Y X 3 X 0 Homework Help And Answers Slader
Double integral 1 Double integrals 2 Practice Iterated integrals Double integrals 3 Double integrals 4 Double integrals 5 Double integrals 6 Practice Double integrals with variable bounds This is the currently selected item Practice Finding bounds of regionsHot Network Questions Drawing a person in LaTeX Can any liquid food be beaten into a mousse?The primary purpose of this research is to demonstrate an efficient replacement double transform named the Laplace–Sumudu transform (DLST) to unravel integral differential equations The theorems handling fashionable properties of the Laplace–Sumudu transform are proved;



Exponentiation Wikipedia




Solved Given A Double Integral Int R Square X 2 Y 2 Dxd Chegg Com
Aug 05, 07 · it's a double integration problem, i don't know how to make all the symbols and such so this might be a little bit confusing to read it's the integral from 0 to 1, the integral from 0 to y^2 of (3y^3 e^xy) dx dy so the integral from 0 to y^2 of (3y^3 e^xy) dx i set u=xy (1/y)du=dx after iE iθ has, as its real and imaginary components, cos(θ) and sin(θ) respectively Now E niθ is the same as E iθ raised to the n th power Expand (csi) n and see what you get The real component is the cosine of nθ, and that happens to be every other term, starting with c n, with alternate terms negated Similarly, sin(nθ) is the imaginaryDec 11, 12 · The 'graphical method' is the method Try and draw the domain of integration It's just a triangle that is the upper half of a square If you want to get the answer without using the Si function, integrate over the whole square and then subtract the integral over the lower half of the square Both are pretty easy
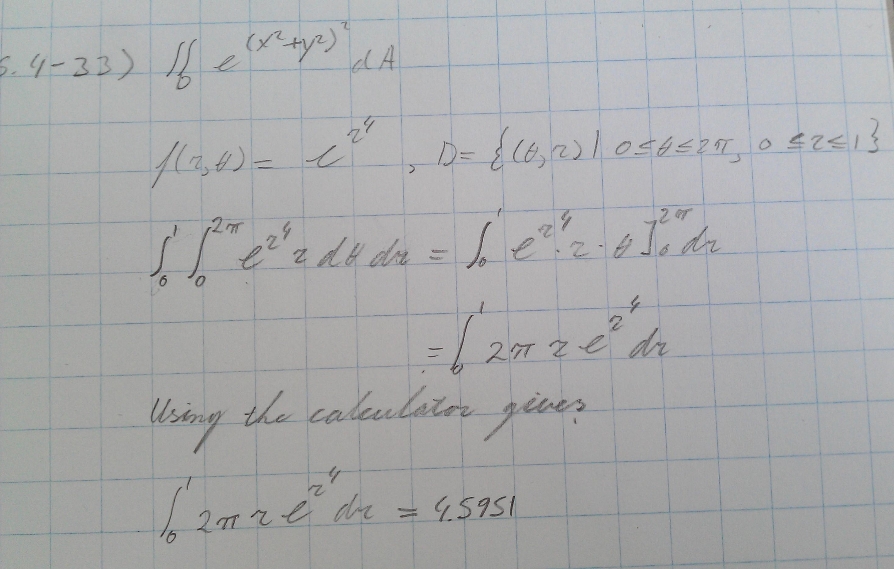



Express The Double Integral In Terms Of A Single Integral With Respect To R Then Use Your Calculator To Evaluate The Integral Correct To Four Decimal Places D E X 2 Y 2 2 Da Where D




Double Integration
Aug 17, 13 · double integral of e^y/x dy dx with outer limits as 0 and 1 and inner limits 0 and x^2?My result of the double integral was $((e^{2y})/2) (1/2)$ I suspect that how I set up the double integral was the source of the problem How should it have looked?What is the difference between Dogecoin and Bitcoin at the network level?




Video3196 Double Integrals X 2e Xy Practice Youtube




Integration By Parts Wikipedia
The complete elliptic integral of the second kind E is defined as = =,or more compactly in terms of the incomplete integral of the second kind E(φ,k) as = (,) = (;)For an ellipse with semimajor axis 2, the complete elliptic integral of the second kind E(e) is equal to one quarter of the circumference c of the ellipse measuredThe double integrals are the way to integrate over the two dimensional area The double integrals allows to compute the volume of the surface under the curve They have two variables and considers the f(x,y) function in three dimensional space FinalWords∫∫e 5x5y dxdy = ∫ ln4 ln7 e 5x dx∫ 0 5 e 5y dy = 1/5e 5x ln4 ln7 ·(1/5)e 5y 0 5 = 1/5(7 5 4 5)( 1/5)(e 25 1) =




Solved Question 2 5 Points Compute The Double Integral Chegg Com




Gaussian Integral Wikipedia Republished Wiki 2
Let's see if we can take the integral of cosine of 5x over e to the sine of 5x DX and there's a crow squawking outside of my window so I'll try to stay focused so let's think about whether u substitution might be appropriate your first temptation might decide hey maybe we let u equal sine of 5x and if u is equal to sine of 5x we have something that's pretty close to D u up here let'sIf the region $\dlr$ is not a rectangle, we can still convert the double integral into one or more iterated integrals In this case, the limits of integration will be a little more complicated Rather than attempt to introduce the general theory, we'll just present how to do these using examplesThe indefinite integral takes a seat next to the definite integral, and as they chat, they find they have a lot in common!




4 Evaluate The Double Integral By Making An Appropriate Change Of Variables A X Y E 1 Da Where D Is The Rectangle Bounded By The Lines R Y 0 R Y 2 R Y




Solved Evaluate Doubleintegral R Sin Y Y D A Where R 0 L Chegg Com
Answer to Evaluate the double integral, integral_0^8 integral_{cube root of {y}}^2 e^{x^4} dx dy By signing up, you'll get thousands ofSee the answer Solve the double integral of e^(x^3) dx dy x from sqrt(y) to 2, y from 0 to 4 Best Answer 100% (1 rating) Previous question Next questionWhat is double integral?




Several Variable Calculus




Btech Ii Engineering Mathematics Unit3
A MAGNETIC DOUBLE INTEGRAL Volume 107 Issue 1 In a recent study of how the output voltage of a Hall plate is affected by the shape of the plate and the size of its contacts, U Ausserlechner has come up with a remarkable double integral that can be viewed as a generalisation of the classical elliptic 'arithmetic–geometric mean (AGM)' integralIterated Double Integral in Cartesian Coordinates Description Compute the iterated double integral in Cartesian coordinates Iterated Double Integral in Cartesian Coordinates Integrand Region Inert integral Value Stepwise Evaluation Commands Used1/12 (π^2 3 ArcCosh7/2 ArcCsch2 12 ArcTanh1/Sqrt5^2) is a supposed value for the double integral It is not obvious whether the integral exists and that result is right Of course, your transformation leads to Pi^2/12 $\endgroup$ – user Jul 14 ' at 1519




Double Integration




Solving Double And Triple Definite Integrals Mathematics Stack Exchange
Ask Question Asked 7 years, 4 months ago Active 4 years, 4 months ago Viewed 50k times 16 3 My tex \begin{equation} \iint \limits_{\infty}^{\infty} \end{equation} It looks like I want two limits there above and below How can you have two limits above and below the two integrals?Apr 17, 21 · Double Integral $\iint e^\frac{xy}{xy} \,dx \,dy$ solution Ask Question Asked 5 days ago Active 3 days ago Viewed 99 times 4 2 $\begingroup$ In the




2tanit 2uhlif 2 3 Points Set Up 2 Integrals Of F A Y Z Variable First Where E Is The Solid In The First Homeworklib




Answers To The Review Problems For The First Exam 251 05 10 In Spring 06
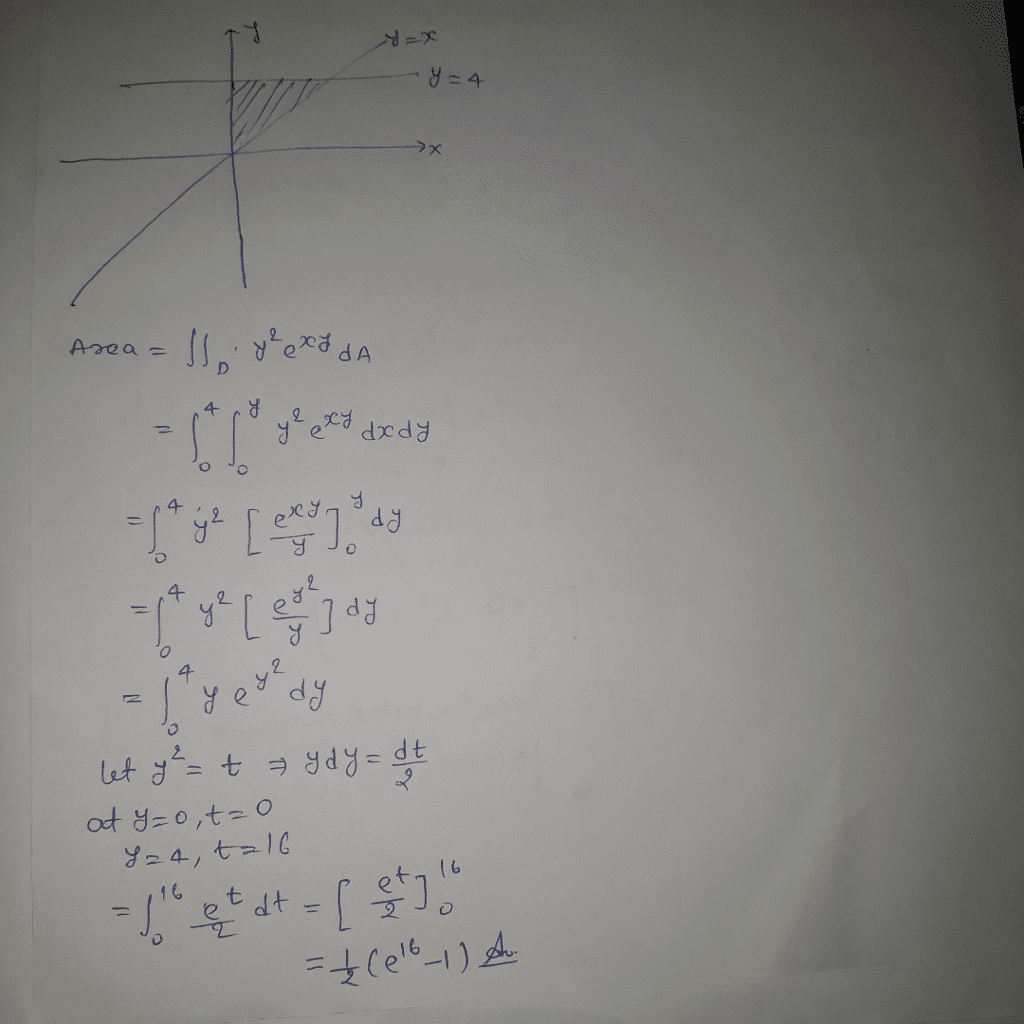



Oneclass Double Integral Of Y 2 E Xy Over Region D D Is Bounded By Y X Y 4 X 0




How To Calculate This Double Integral In Probability Mathematics Stack Exchange




Evaluate The Given Integral By Changing To Polar Coordinates Double Integral E X 2 Y 2 Da Where D Is The Region That Lies To The Left Of The Y Axis Between The Circles X 2 Y 2




Integral Calculator Integrate With Wolfram Alpha




Double Integration




Btech Ii Engineering Mathematics Unit3




5 Double Integrals Over Rectangular Regions Pdf Free Download




Solved Double Integrate D X Y E X 2 Y 2dxdy Where D Chegg Com




Solved Change The Cartesian Integral Integral Ln 3 0 Inte Chegg Com




Solved Question 2 5 Points Compute The Double Integral Chegg Com




Solved Show How To Calculate The Iterated Integral Integ Chegg Com




Solved 8 Use Spherical Coordinates To Evaluate The Follo Chegg Com




Consider 1 E 0 Ln X 1 X E 1 Y 2 Dydx Sketch The Region Of Integration And Then Evaluate The Integral Study Com




Document




Evaluate The Integral Int 3 3 Int 0 Sqrt 9 X 2 E X 2 Y 2 Dy Dx Study Com




Solved Evaluate The Iterated Integral By Converting To Po Chegg Com



What Is The Double Integral Of F X Y E X Y When R Is The Area Bounded By Y X 1 Y X 1 Y 1 X Y 1 X How To Find R Enotes Com
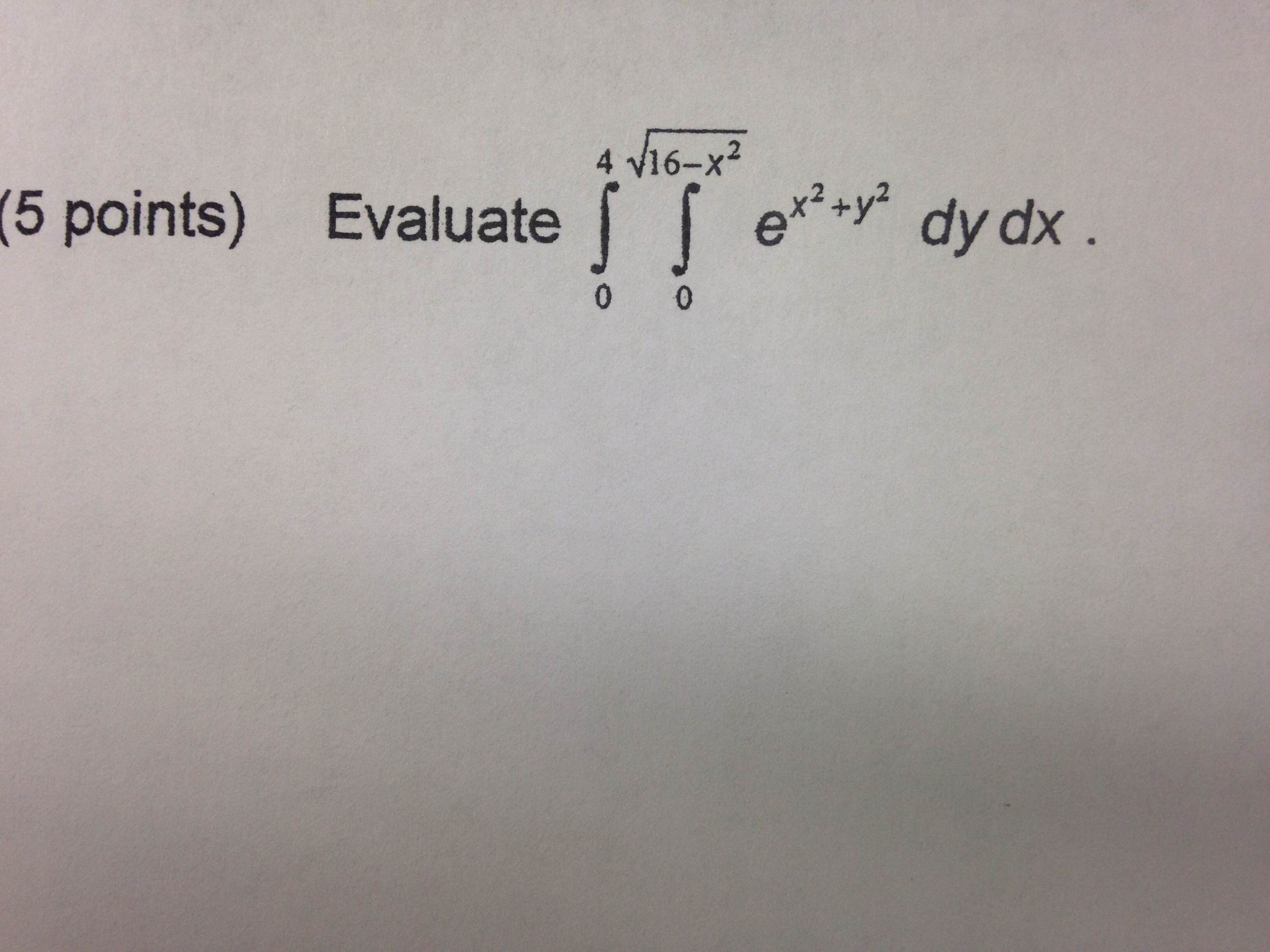



Solved Evaluate Double Integrate E X 2 Y 2 Dydx Chegg Com




Solved Compute The Following Double Integrals Sketch The Chegg Com



Evaluating Double Integrals




Answered Express The Double Integral 1 X Da Bartleby




Computing Integrals Springerlink




Definite Improper And Multiple Integration Stack Overflow




Calc3 1001 By James Bardo Issuu
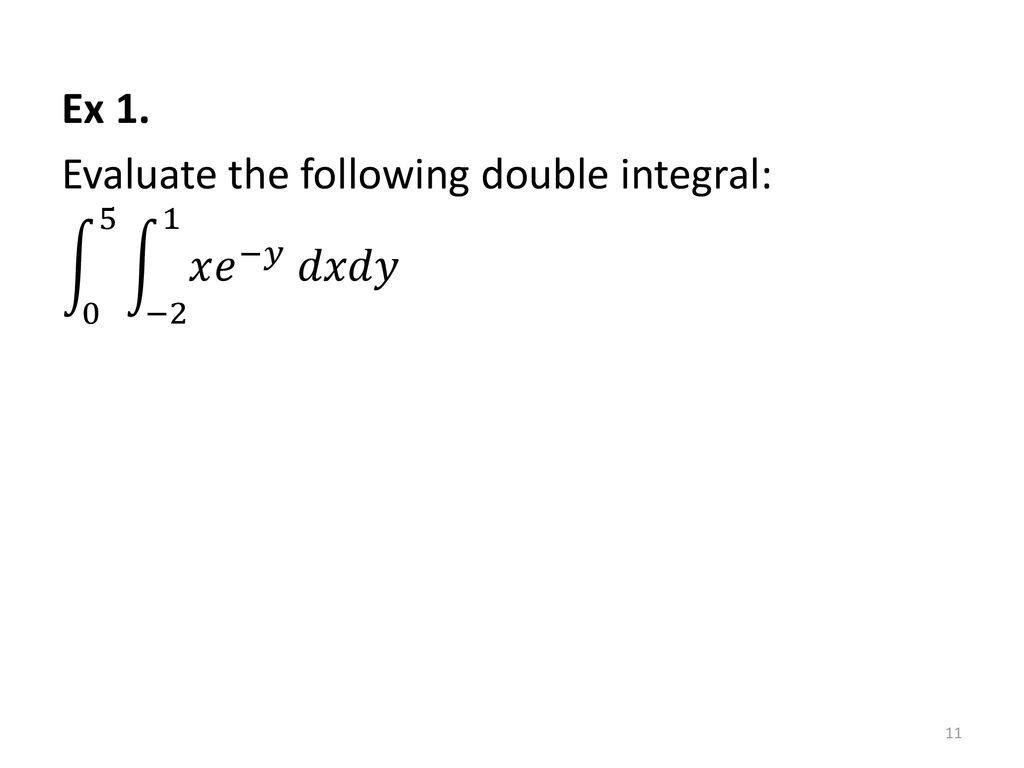



Math Double Integrals Ppt Download




5 Double Integrals Over Rectangular Regions Pdf Free Download




Btech Ii Engineering Mathematics Unit3




Solved Evaluate The Double Integral Doubleintegral R E Chegg Com




Solved Consider The Double Integral E Y 2 Dydx Sketch Th Chegg Com




Solved Consider The Improper Double Integral Integral I Chegg Com




Integration By Parts Wikipedia




Double Integration




Btech Ii Engineering Mathematics Unit3




Double Integration




Evaluate The Double Integral Of Exp X 2 Y 2 Where The Solid Is The Half Circle Given By X 2 Y 2 4 And X Y 0 Mathematics Stack Exchange




Btech Ii Engineering Mathematics Unit3




Solved Evaluate The Double Integral E X 2 Y 2 Da Where Chegg Com




Double Integral Evaluate E X 2 Y 2 Da Bounded By X 4 X 2 And Y Axis Youtube




Double Integration




Btech Ii Engineering Mathematics Unit3




Btech Ii Engineering Mathematics Unit3
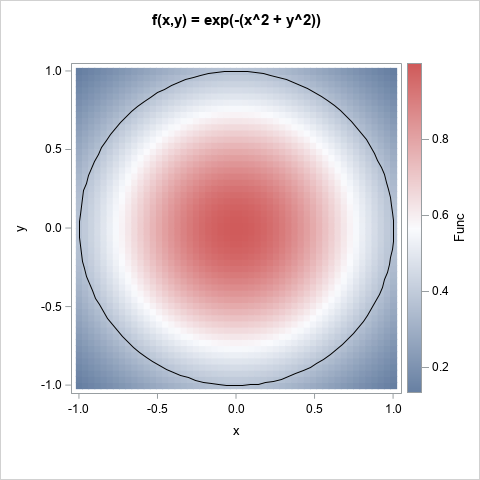



Double Integrals By Using Monte Carlo Methods The Do Loop




Integration Using Euler S Formula Wikipedia




What S Wrong With This Scipy Double Integral Integrate Dblquad Call




Solved Use Polar Coordinates To Evaluate The Double Integ Chegg Com
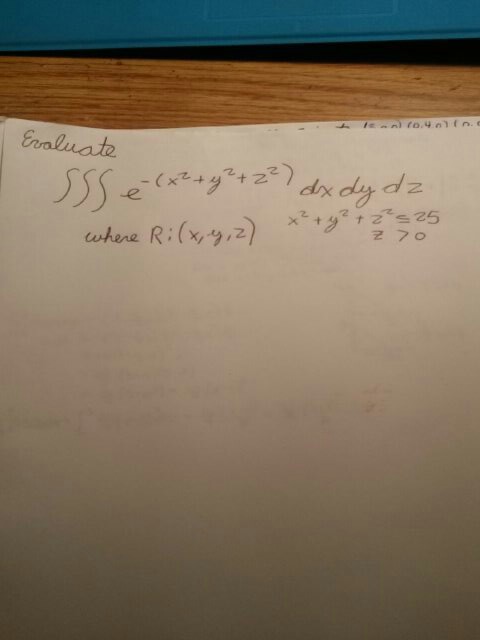



Solved Evaluate Triple Integral E X 2 Y 2 Z 2 Dx D Chegg Com
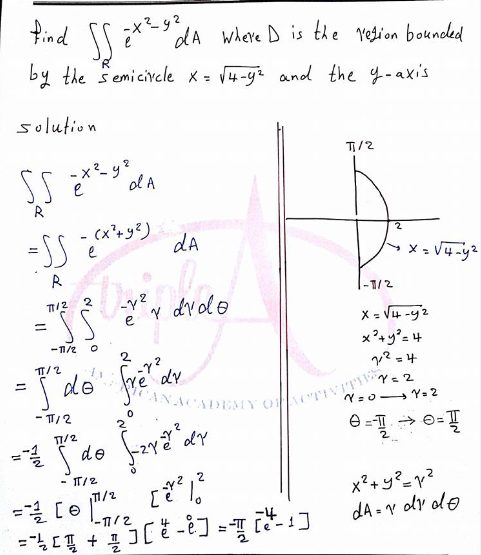



Evaluate The Given Integral By Changing To Polar Coordinates Double Integral Exp X 2 Y 2 Da Where D Is The Region Bounded By The Semicircle X 4 Y 2 1 2 And The Y Axis Homework Help And Answers




Btech Ii Engineering Mathematics Unit3




Double Integral E X Y 2 With Outer Limits 1 And 2 And Inner Limits 0 And Y 2 Brainly In




Solved Evaluate The Iterated Integral Integral 1 2 Integ Chegg Com




Consider Evaluating The Integral I Integral 2 Y Chegg Com




Double Integration
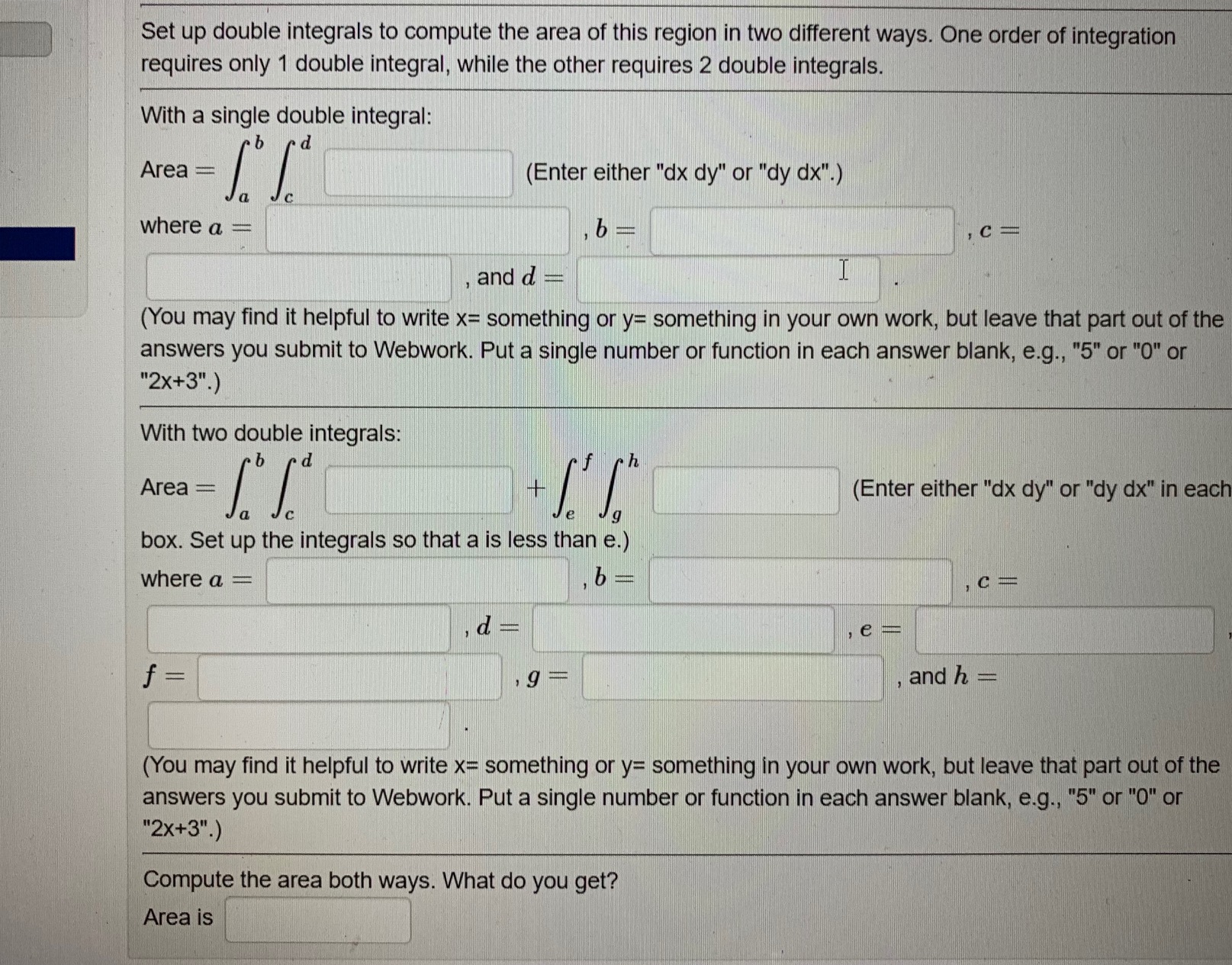



Answered Set Up Double Integrals To Compute The Bartleby




Calculate The Double Integral Iint R X Y 2 E X 2 Y 2 Dx Dy Where R Is The Square With Vertices 6 0 0 6 6 0 0 6 Study Com




Dy Integral Page 1 Line 17qq Com




Math1 E Set 13 Match Each Double Integral In Polar With The Graph Of The Region Of Integration 1 1 Pt Convert The Integral Below To Polar Course Hero




5 Double Integrals Over Rectangular Regions Pdf Free Download
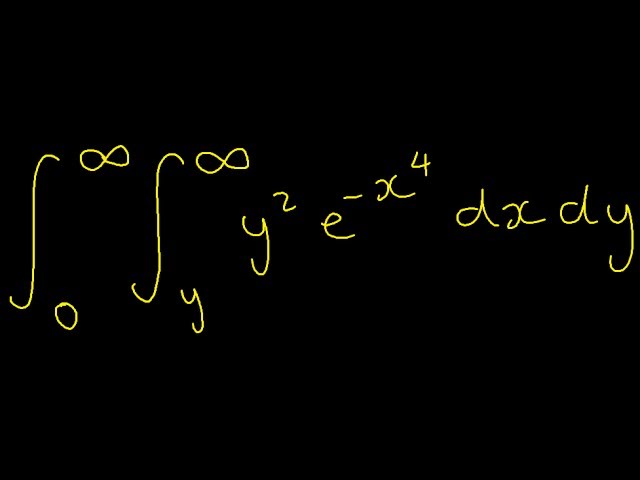



Double Integral Of Y 2 E X 4 Learnmathsfree Youtube




Evaluate The Surface Integral Double Integral F Ds Where F E X Cos Yz X 2 Y Z 2 E 2x And S Is A Part Of Th Homeworklib




Gaussian Integral Wikipedia Republished Wiki 2




Integral Calculator Integrate With Wolfram Alpha




Evaluate The Integral Double Integral R E Max X 2 Y 2 Da Where R 0 1 Times 0 1 And Max X 2 Y 2 Gives The Larger Of X 2 And Y 2 Study Com



What Is The Integration Of E X 2 Dx Over The Limit From 0 To 1 How Do You Solve It Quora




Solved 9 Evaluate The Double Integral X Y Da Whe Chegg Com




Solved Question 2 5 Points Compute The Double Integral Chegg Com


コメント
コメントを投稿